Definition Math Kernel

So you know what a function is im assuming.

Delta math quiz. An important special case is the kernel of a linear mapthe kernel of a matrix also called the null space is the kernel of the linear map defined by the matrix. Ker o g in g. The theory of positive definite kernels extends the theory of positive definite functions cf.

Kernel linear algebra or null space a set of vectors mapped to the zero vector. How to use kernel in a sentence. Kernel definition is the inner softer part of a seed fruit stone or nut.

Cohn universal algebra kluwer 1981 isbn 90 277 1213 1. Kernel set theory an equivalence relation. Positive definite function on groups.

Kerf is therefore a subset of a the related image of a function is defined by imffxx in a. For a function f on a group g to be positive definite it is necessary and sufficient that the function k x y f xy 1 on g times g is a positive definite kernel. That is a correct definition.

Og 0 and then we might even call the kernel the set of elements killed by o. In algebra the kernel of a homomorphism function that preserves the structure is generally the inverse image of 0 except for groups whose operation is denoted multiplicatively where the kernel is the inverse image of 1. Kernel category theory a generalization of the kernel of a homomorphism.

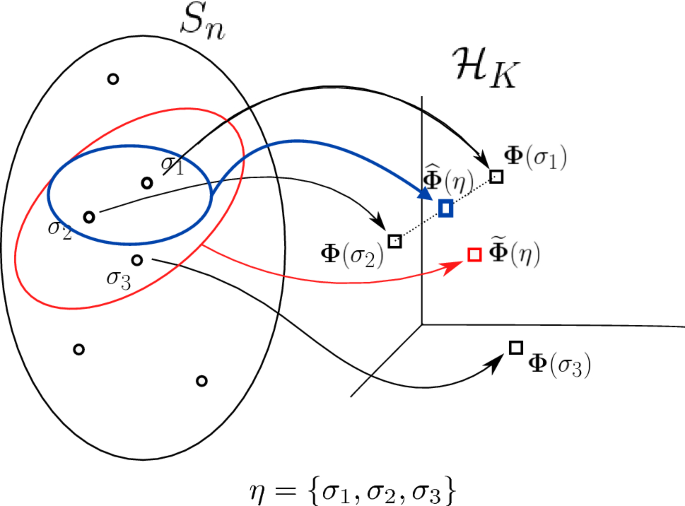
I give some context here for why we use kernels. Partition by image under a function. Basically kernels are the things that go to zero under some function.

Kernel may mean a subset associated with a mapping which measures how far it is from being injective or being a monomorphism. The kernel of a mapping is the set of elements that map to the zero element such as zero or zero vector as in kernel of a linear operator and kernel of a matrix. For any function fa b where a and b are any sets the kernel also called the null space is defined by kerfxx in asuch thatfx0 so the kernel gives the elements from the original set that are mapped to zero by the function.

When the groups are abelian we often write 0 zero for the identity element. Its a thing that takes an element of one set and associates with it an elem. In this case it would be.