Delta Math Linear Regression
Delta Math Linear Regression, Indeed recently has been hunted by consumers around us, perhaps one of you personally. People now are accustomed to using the internet in gadgets to view video and image information for inspiration, and according to the name of this article I will discuss about
If the posting of this site is beneficial to our suport by spreading article posts of this site to social media marketing accounts which you have such as for example Facebook, Instagram and others or can also bookmark this blog page.
Https Wcpss Instructure Com Courses 370801 Files 15817408 Download Verifier 4e8teqaljvgjhac8rxo3hxhhlu96kef7bdiysv4c Wrap 1 Belur Math Kahan Hai
Risks Free Full Text Delta Boosting Implementation Of Negative Binomial Regression In Actuarial Pricing Html Belur Math Kahan Hai
Gradient Descent For Linear Regression One Variable In Octave Stack Overflow Belur Math Kahan Hai
Polynomial Curve Fitting Matlab Polyfit Belur Math Kahan Hai
Basics Of Mathematical Notation For Machine Learning Belur Math Kahan Hai
Application Of The Common Base Method To Regression And Analysis Of Covariance Ancova In Qpcr Experiments And Subsequent Relative Expression Calculation Bmc Bioinformatics Full Text Belur Math Kahan Hai
To bring this back to our somewhat ludicrous garden gnome example we could create a regression with the east west location of the garden gnome as the independent.
Belur math kahan hai. Samuel forlenza phd recommended for you. Its statistical application can be traced as far back as 1928 by t. Or the regression function fx.
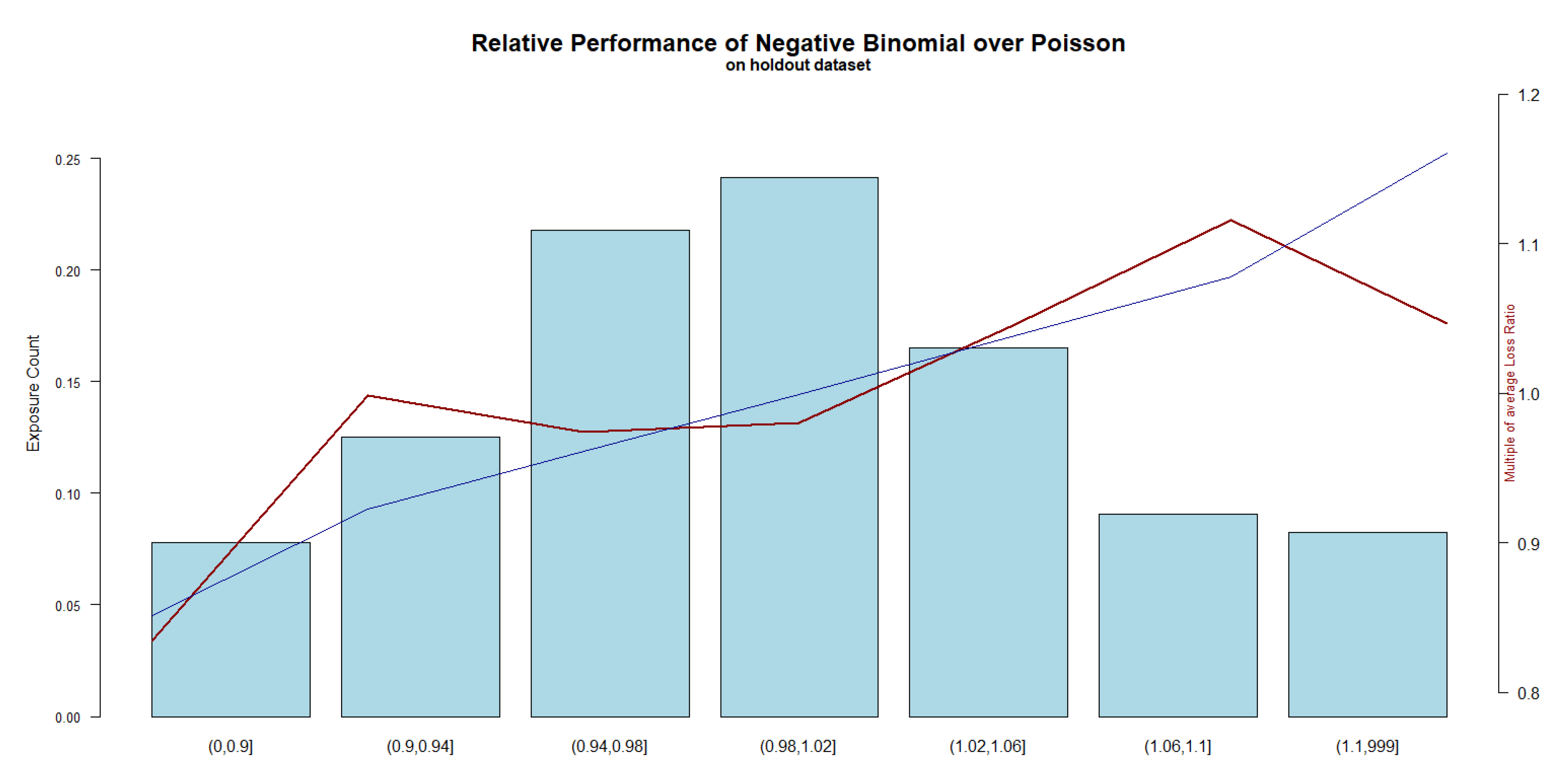
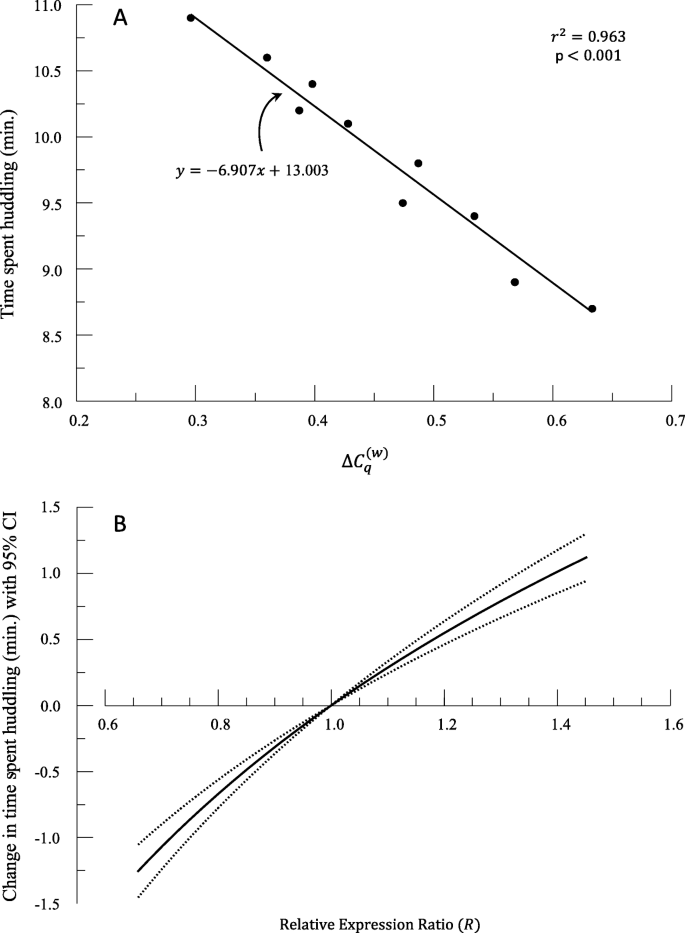
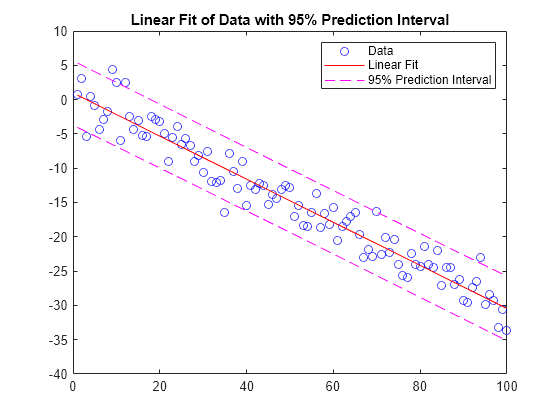
The least squares method finds the values of the y intercept and slope that make the sum of the squared residuals also know as the sum of squared errors or sse as small as possible. Details iteration distribution condence intervals weight loss data p. Robert dorfman also described a version of it in 1938.
The most common method of constructing a simple linear regression line and the only method that we will be using in this course is the least squares method. Apa style 7th edition. An access code gives you full access to the entire library of deltamath content and instructional videos.
The linear regression is exact in the case when the two dimensional distribution of the variables x and y is normal. X delta where u x mathsf e y mid x x where x and delta are independent random variables. 311 nonlinear regression models we have usually assumed regression is of the form yi 0 px 1 j1 jxij i.
Delta method nonlinear regression nonlinear regression. Now there are a few additional equations you will have to know with gradient descent iweight. Reference lists journal articles books reports theses websites more duration.
In other words numbers alpha and beta solve the following minimization problem. Such a line that minimizes the sum of squared residuals of the linear regression model. Linear regression creates a linear mathematical relationships between these two variables.
A teacher code is provided by your teacher and gives you free access to their assignments. While the delta method generalizes easily. A formal description of the method was presented by j.
It enables calculation predicting the dependent variable if the dependent variable is known. Linear regression yb0b1x where b0 is the slope b1 is the weight of independent feature x. Here best will be be understood as in the least squares approach.
Pre calculus find the linear regression line using the ti 8384 calculator duration. 0 px 1 j1 jxj is linear in beta.
Multiple Linear Regression Analysis For Delta Download Scientific Diagram Belur Math Kahan Hai
Polynomial Curve Fitting Matlab Polyfit Belur Math Kahan Hai
How To Use The Statistics Calculator In Delta Math Youtube Belur Math Kahan Hai
Pdf An Alternative Algorithm And R Programming Implementation For Least Absolute Deviation Estimator Of The Linear Regression Models Belur Math Kahan Hai